Ряды фурье для чайников скачать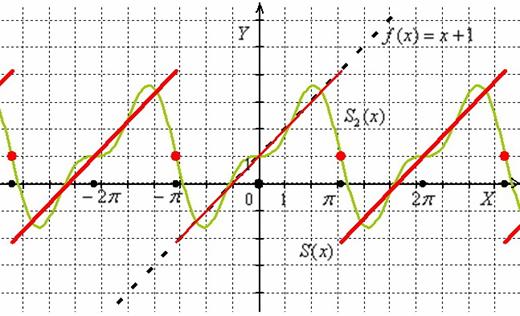
Ряды фурье для чайников.Идея о том, что любая периодическая функция может быть представлена в виде ряда гармонически связанных синусов и косинусов была предложена бароном Жан Батистом Жозефом Фурье (\(1768-1830\)). Чтобы рассмотреть эту идею более детально, введем базовые определения. Предположим, что функция \(f\left( x \right)\) с периодом \(2\pi\) абсолютно интегрируема в интервале \(\left[ \right].\) При этом является конечным так называемый интеграл Дирихле : \[\int\limits_ ^\pi \right|dx> ряд Фурье для функции \(f\left( x \right)\) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье ). Разложение в ряд Фурье четной функции \(f\left( x \right)\) с периодом \(2\pi\) не содержит синусов и имеет вид \[f\left( x \right) = \frac >> + \sum\limits_ ^\infty \cos nx> ,\] где коэффициенты Фурье определяются выражениями \[ = \frac \int\limits_0^\pi ,>\;\; = \frac \int\limits_0^\pi .> \] Аналогично, разложение в ряд Фурье нечетной функции \(f\left( x \right),\) имеющей период \(2\pi,\) содержит только синусы и имеет вид \[f\left( x \right) = \sum\limits_ ^\infty \sin nx> ,\] где коэффициенты \( >\) равны \[ = \frac \int\limits_0^\pi .\] Ниже мы рассмотрим некоторые типичные примеры разложения функций с периодом \(2\pi\) в ряд Фурье, предполагая, что такие разложения существуют и сходятся к заданной функции. | |
|
Скачать Скачать | |
| Новинки: | |